值得一提的，深度优先算法用到了回溯的算法思想，这个算法虽然相对比较简单，但很重要，在生产上广泛用在正则表达式，编译原理的语法分析等地方，很多经典的面试题也可以用回溯算法来解决，如八皇后问题，排列组合问题，0-1背包问题，数独问题等，也是一种非常重要的算法。

本文将会从以下几个方面来讲述回溯算法，相信大家看了肯定有收获！

什么是回溯算法

回溯算法本质其实就是枚举，在给定的枚举集合中，不断从其中尝试搜索找到问题的解，如果在搜索过程中发现不满足求解条件，则「回溯」返回，尝试其它路径继续搜索解决，这种走不通就回退再尝试其它路径的方法就是回溯法，许多复杂的，规模较大的问题都可以使用回溯法，所以回溯法有「通用解题方法」的美称。

回溯算法解题通用套路

为了有规律地求解问题，我们把问题分成多个阶段，每个阶段都有多个解，随机选择一个解，进入下一个阶段，下一个阶段也随机选择一个解，再进入下一个阶段…

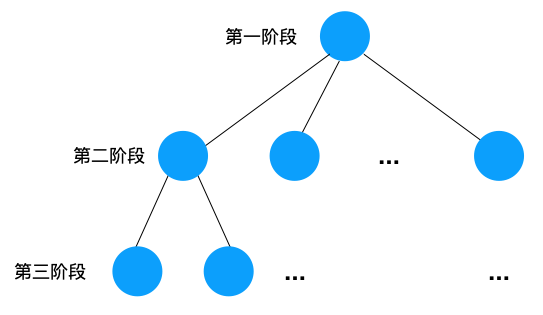
每个阶段选中的解都放入一个「已选解集合」中，并且要判断「已选解集合」是否满足问题的条件（base case）,有两种情况

如果「已选解集合」满足问题的条件，则将「已选解集合」放入「结果集」中，并且「回溯」换个解再遍历。
如果不满足，则「回溯」换个解再遍历。

根据以上描述不难得出回溯算法的通用解决套路伪代码如下:


function backtrace(已选解集合,每个阶段可选解) {
    if (已选解集合满足条件) {
        结果集.add(已选解集合);
        return;
    }

    // 遍历每个阶段的可选解集合
    for (可选解 in 每个阶段的可选解) {

        // 选择此阶段其中一个解,将其加入到已选解集合中
        已选解集合.add(可选解)

        // 进入下一个阶段
        backtrace(已选解集合,下个阶段可选的空间解)

        // 「回溯」换个解再遍历
        已选解集合.remove(可选解)

    }
}

通过以上分析我们不难发现回溯算法本质上就是深度优先遍历，它一般解决的是树形问题（问题分解成多个阶段，每个阶段有多个解，这样就构成了一颗树），所以判断问题是否可以用回溯算法的关键在于它是否可以转成一个树形问题。

另外我们也发现如果能缩小每个阶段的可选解，就能让问题的搜索规模都缩小，这种就叫「剪枝」，通过剪枝能有效地降低整个问题的搜索复杂度！

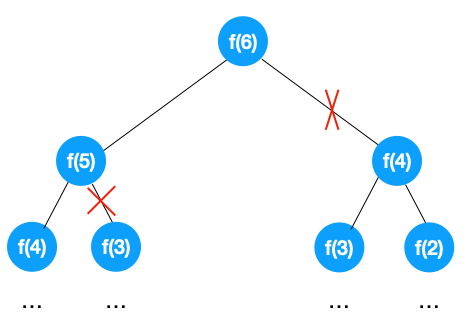
综上，我们可以得出回溯算法的基本套路如下：

将问题分成多个阶段，每个阶段都有多个不同的解，这样就将问题转化成了树形问题，这一步是问题的关键！如果能将问题转成树形问题，其实就成功了一半，需要注意的是树形问题要明确终止条件，这样可以在 DFS 的过程中及时终止遍历，达到剪枝的效果
套用上述回溯算法的解题模板，进行深度优先遍历，直到找到问题的解。

只要两个步骤，是不是很简单！接下来我们套用以上的解题模板来看看怎么使用以上回溯算法解题套路来解几道经典的问题。

经典习题讲解

0-1背包问题

这里介绍一下一种比较简单的背包问题：

有一个背包，背包总的承载重量是 Wkg。现在我们有 n 个物品，每个物品的重量不等，并且不可分割。我们现在期望选择几件物品，装载到背包中。在不超过背包所能装载重量的前提下，如何让背包中物品的总重量最大？假设这 n 个物品的质量分别 3kg, 4kg, 6kg, 8kg，背包总的承载重量是 10kg。

1、将问题转为树形结构

由于有 n 个物品，所以问题可以分解成 n 个阶段，第一个阶段可以有 n 个物品可选，第二个阶段有 n-1 个物品可选,,,,,,最后一个阶段有 1 个物品可选，不难画出以下递归树。

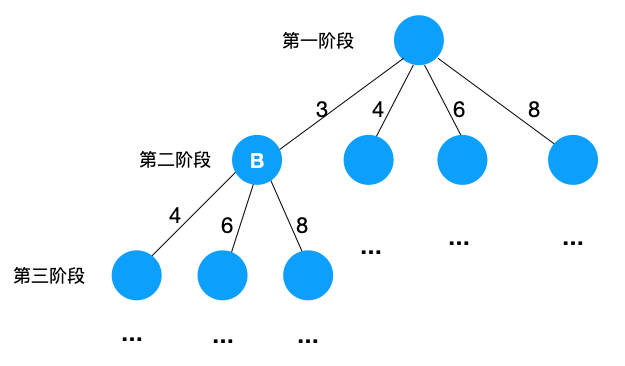
既然能转成树形结构，那我们进入步骤 2

2、套用上述回溯算法的解题模板，进行深度优先遍历，直到找到问题的解

需要注意的，进行 DFS 的终止条件是什么呢，显然是所选物品质量（遍历的节点）和大于等于背包质量，稍加变形不难得出以下代码

public class Solution {
    /**
     * 结果集
     */
    private static Integer RESULT = 0;

    /**
     * 背包最大承载质量
     */
    private static Integer KNAPSACK_MAX_WEIGHT = 10;

    /**
     * 现有背包
     */
    private static List<Integer> WEIGHTS = Arrays.asList(3, 4, 6, 8);

    /**
     * 遍历当前阶段的解
     *
     * @param selectedWeights  已选解集合
     * @param selectableWeight 可选的解集合
     */
    public static void knapsack(List<Integer> selectedWeights, List<Integer> selectableWeight) {

        {
            // 求已选物品的总重量
            int sumOfWeights = selectedWeights.stream().mapToInt(Integer::intValue).sum();
            if (sumOfWeights == KNAPSACK_MAX_WEIGHT) {
                RESULT = Math.max(RESULT, sumOfWeights);
                return;
            } else if (sumOfWeights > KNAPSACK_MAX_WEIGHT) {
                // 如果已选物品的总重量超过背包最大承受质量，则要把最后一个选择的物品移除，再求质量和
                selectedWeights.remove(selectedWeights.size() - 1);
                sumOfWeights = selectedWeights.stream().mapToInt(Integer::intValue).sum();
                RESULT = Math.max(RESULT, sumOfWeights);
                return;
            } else {
                RESULT = Math.max(RESULT, sumOfWeights);
            }
        }

        // 遍历每个阶段的可选解集合
        for (int i = 0; i < selectableWeight.size(); i++) {
            Integer num = selectableWeight.get(i);

            // 去除不符合条件的解，减枝
            if (selectedWeights.contains(num)) {
                continue;
            }

            // 选择子节点的其中一个解
            selectedWeights.add(num);

            // 选完之后再进行 dfs
            knapsack(selectedWeights, selectableWeight);

            // 「回溯」换个解再遍历
            selectedWeights.remove(num);
        }

    }

    public static void main(String[] args) {
        List<Integer> selectedNums = new ArrayList<>();
        knapsack(selectedNums, WEIGHTS);
        System.out.println("result = " + RESULT);
    }
}

可以看到套用模板我们又轻松解决了0-1背包问题，可能有人会说以上问题比较简单，接下来我们来看看如何用上模板来解八皇后问题。