N叉树,即相对于二叉树最多拥有不止2个子节点的树:
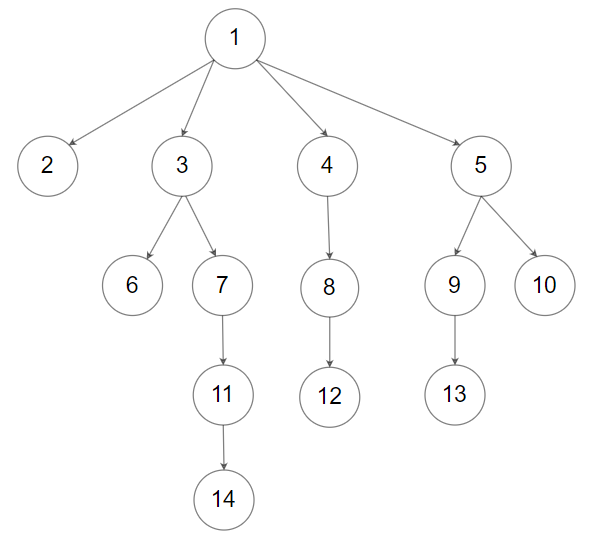
下面是N叉树的遍历,前序、后序、深度、广度变量完整实现。
public class PolyTree {
/**
* 深度优先需要构建一个后进先出的栈
*
* @param root
*/
public List<String> depthFirst(PolyNode root) {
List<String> res = new ArrayList<String>();
Deque<PolyNode> nodeDeque = new LinkedList<>();
PolyNode node = root;
nodeDeque.push(node);
while (!nodeDeque.isEmpty()) {
node = nodeDeque.pop();
res.add(node.getName());
List<PolyNode> children = node.getChildren();
//注意这里要从后向前遍历
for (int i = children.size() - 1; i >= 0; i--) {
//从头压入
nodeDeque.push(children.get(i));
}
}
return res;
}
/**
* 广度优先需要构建一个先进先出的队列
*
* @param root
*/
public List<String> breadthFirst(PolyNode root) {
List<String> res = new ArrayList<String>();
Deque<PolyNode> nodeDeque = new LinkedList<>();
PolyNode node = root;
nodeDeque.add(node);
while (!nodeDeque.isEmpty()) {
node = nodeDeque.pop();
res.add(node.getName());
nodeDeque.addAll(node.getChildren());
}
return res;
}
/**
* 递归版后序
*/
public List<String> postorderRecursion(PolyNode root) {
List<String> res = new ArrayList<String>();
if (root == null) {
return res;
}
for (PolyNode child : root.getChildren()) {
preorderRecursion(child);
}
res.add(root.getName());
return res;
}
/**
* 迭代的方法得到 N 叉树的后序遍历。
*
* 在后序遍历中,我们会先遍历一个节点的所有子节点,再遍历这个节点本身。
*
* 例如:当前的节点为 u,它的子节点为 v1, v2, v3 时,那么后序遍历的结果为
*
*
* [children of v1], v1, [children of v2], v2, [children of v3], v3, u
* 其中 [children of vk] 表示以 vk 为根节点的子树的后序遍历结果(不包括 vk)。
*
* 将结果反转,得到
*
*
* u, v3, [children of v3]', v2, [children of v2]', v1, [children of v1]'
* 其中 [a]' 表示 [a] 的反转。
*
* 此时我们发现,结果和前序遍历非常类似,只不过前序遍历中对子节点的遍历顺序是 v1, v2, v3,而这里是 v3, v2, v1。
*
* 因此我们可以使用和 N叉树的前序遍历 相同的方法,使用一个栈来得到后序遍历。我们首先把根节点入栈。
*
* 当每次我们从栈顶取出一个节点 u 时,就把 u 的所有子节点顺序推入栈中。
* 例如 u 的子节点从左到右为 v1, v2, v3,那么推入栈的顺序应当为 v1, v2, v3,这样就保证了下一个遍历到的节点(即 u 的第一个子节点 v3)出现在栈顶的位置。
* 在遍历结束之后,我们把遍历结果反转,就可以得到后序遍历。
*
* 时间复杂度:时间复杂度:O(M)O(M),其中 MM 是 N 叉树中的节点个数。每个节点只会入栈和出栈各一次。
*
* 空间复杂度:O(M)O(M)。在最坏的情况下,这棵 N 叉树只有 2 层,所有第 2 层的节点都是根节点的孩子。
* 将根节点推出栈后,需要将这些节点都放入栈,共有 M - 1M−1 个节点,因此栈的大小为 O(M)O(M)。
*
*
*
* @param root
*/
public List<String> postorder(PolyNode root) {
LinkedList<String> res = new LinkedList<>();
if (root == null) {
return res;
}
Deque<PolyNode> stack = new ArrayDeque<>();
stack.addLast(root);
while (!stack.isEmpty()) {
PolyNode node = stack.removeLast();
res.addFirst(node.getName());
for (int i = 0; i < node.getChildren().size(); i++) {
stack.addLast(node.getChildren().get(i));
}
}
return res;
}
/**
* 迭代实现:直接反转先序结果即可
*
* @param root
*/
public List<String> postorderByReverse(PolyNode root) {
List<String> res_pre = new ArrayList<>();
if (root == null) {
return res_pre;
}
Stack<PolyNode> s = new Stack<>();
s.push(root);
while (!s.isEmpty()) {
PolyNode n = s.pop();
res_pre.add(n.getName());
for (PolyNode node : n.getChildren()) {
s.push(node);
}
}
Collections.reverse(res_pre);
return res_pre;
}
/**
* 迭代的方法得到 N 叉树的前序遍历。
* 我们使用栈来帮助我们得到前序遍历,需要保证栈顶的节点就是我们当前遍历到的节点。
* 我们首先把根节点入栈,因为根节点是前序遍历中的第一个节点。随后每次我们从栈顶取出一个节点 u,它是我们当前遍历到的节点,并把 u 的所有子节点逆序推入栈中。
* 例如 u 的子节点从左到右为 v1, v2, v3,那么推入栈的顺序应当为 v3, v2, v1,这样就保证了下一个遍历到的节点(即 u 的第一个子节点 v1)出现在栈顶的位置。
*
* 时间复杂度:时间复杂度:O(M)O(M),其中 MM 是 N 叉树中的节点个数。每个节点只会入栈和出栈各一次。
*
* 空间复杂度:O(M)O(M)。在最坏的情况下,这棵 N 叉树只有 2 层,所有第 2 层的节点都是根节点的孩子。
* 将根节点推出栈后,需要将这些节点都放入栈,共有 M - 1M−1 个节点,因此栈的大小为 O(M)O(M)。
*
* @param root
*/
public List<String> preorder(PolyNode root) {
LinkedList<String> output = new LinkedList<>();
if (root == null) {
return output;
}
LinkedList<PolyNode> stack = new LinkedList<>();
stack.add(root);
while (!stack.isEmpty()) {
PolyNode node = stack.pollLast();
output.add(node.getName());
Collections.reverse(node.getChildren());
for (PolyNode item : node.getChildren()) {
stack.add(item);
}
}
return output;
}
/**
* 递归版前序
* 如果树太深的话,会出现java.lang.StackOverflowError
*/
public List<String> preorderRecursion(PolyNode root) {
List<String> res = new ArrayList<String>();
if (root == null) {
return res;
}
res.add(root.getName());
for (PolyNode child : root.getChildren()) {
preorderRecursion(child);
}
return res;
}
public static void main(String[] args) {
PolyNode root = makeTree();
List<String> strings = new PolyTree().depthFirst(root);
for (String s : strings) {
System.out.println(s);
}
}
public static PolyNode makeTree() {
PolyNode root = new PolyNode("A", null);
PolyNode B = new PolyNode("B", root);
PolyNode C = new PolyNode("C", root);
PolyNode D = new PolyNode("D", root);
root.addChild(B);
root.addChild(C);
root.addChild(D);
PolyNode E = new PolyNode("E", B);
PolyNode F = new PolyNode("F", B);
B.addChild(E);
B.addChild(F);
PolyNode G = new PolyNode("G", D);
D.addChild(G);
PolyNode H = new PolyNode("H", E);
PolyNode I = new PolyNode("I", E);
PolyNode J = new PolyNode("J", E);
E.addChild(H);
E.addChild(I);
E.addChild(J);
return root;
}
}