回文串

回文指一个顺着读和反过来读都一样的字符串，比如madam、我爱我，这样的短句。

最长回文子串

题目描述：
给定一个字符串，求它的最长回文子串。

解法1

如果一段字符串是回文，那么以某个字符为中心的前缀和后缀都是相同的。
我们可以枚举每个字符，以此为中心判断其前缀和后缀是否相同，记录最长的回文长度和中心字符位置。从而得到最长字符子串！

首先通过在每个字符的两边都插入一个特殊的符号，将所有可能的奇数或偶数长度的回文子串都转换成了奇数长度。比如 abba 变成 #a#b#b#a#， aba变成 #a#b#a#。
此外，为了进一步减少编码的复杂度，可以在字符串的开始加入另一个特殊字符，这样就不用特殊处理越界问题，比如$#a#b#a#。

实现如下：

     public static String getMaxPalindromeSub(String source) {
        char[] s = source.toCharArray();
        int maxIndex = 0;//记录最长回文字符的中心位置
        int maxLen = 0;//记录最长回文子串长度
        for (int i = 0; i < s.length; i++) {
            int left = i;//向左扩展指针
            int right = i;//向右扩展指针
            int curLen = 0;//当前回文字符长度
            while (left > 0 && right < s.length && s[left--] == s[right++]) {
                curLen++;
            }
            if (maxLen < curLen) {
                maxIndex = i;
                maxLen = curLen;
            }
        }
        return source.substring(maxIndex - maxLen + 1, maxIndex + maxLen);//注意边界
    }

解法2 Manacher算法

下面以字符串12212321为例，为了避免处理边界，降低复杂度，经过预处理变成了 S[] = "$#1#2#2#1#2#3#2#1#";
然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度（包括S[i]，也就是把该回文串“对折”以后的长度），比如S和P的对应关系：

S  #  1  #  2  #  2  #  1  #  2  #  3  #  2  #  1  #
P  1  2  1  2  5  2  1  4  1  2  1  6  1  2  1  2  1
(p.s. 可以看出，P[i]-1正好是原字符串中回文串的总长度）

那么怎么计算P[i]呢？该算法增加两个辅助变量（其实一个就够了，两个更清晰）id和mx，其中 id 为已知的 {右边界最大} 的回文子串的中心，mx则为id+P[id]，也就是这个子串的右边界。

我们可以得到如下结论：

//记j = 2 * id - i，也就是说 j 是 i 关于 id 的对称点(j = id - (i - id))
if (mx - i > P[j])
    P[i] = P[j];
else /* P[j] >= mx - i */
    P[i] = mx - i; // P[i] >= mx - i，取最小值，之后再匹配更新。

即如果mx > i，那么P[i] >= MIN(P[2 * id - i], mx - i)。这就是这个算法的关键点了。这里很容易被卡住！

光看上面代码还是不够清晰，我们借助图来理解比较容易：

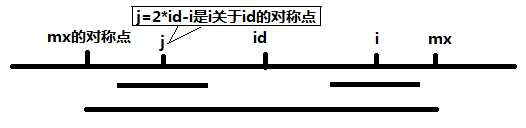
当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。

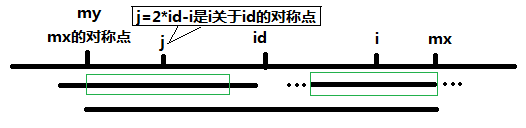
当 P[j] >= mx - i 的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能老老实实去匹配了。

对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了。

实现如下：

    /**
     * @param source 已处理为$#a#b#c#b#c#^ (首部加$,尾部加^,中介用#隔开)格式
     *               注意$,#,^特殊字符都不能在原字符中出现，如果在原来字符串里面就包含这些字符，可以选择其他不包含的字符替代
     * @return 最大回文子串
     */
    private static String getMaxPalindromeSubString(String source) {
        char[] s = source.toCharArray();
        int length = s.length;
        if (length <= 1) {
            return source;
        }
        int[] p = new int[length];// p[i] 来记录以字符s[i]为中心的最长回文子串向左/右扩张的长度
        int id = 0;//id 为已知的 {右边界最大} 的回文子串的中心
        int mx = 0;//mx则为id+p[id]，也就是这个子串的右边界
        for (int i = 1; i < length - 1; i++) {
            int j = 2 * id - i;
            p[i] = mx > i ? Math.min(p[j], mx - i) : 1;
            while (s[p[i] + i] == s[i - p[i]]) {
                p[i]++;
            }
            if (p[i] + i > mx) {
                mx = i + p[i];
                id = i;
            }
        }
        int index = 0;
        int maxLen = 1;
        for (int i = 0; i < length; i++) {
            if (p[i] > maxLen) {
                maxLen = p[i];
                index = i;
            }
        }
        return source.substring(index - maxLen + 1, index + maxLen);
    }