末日期权(End of Day Options)是一种期权合约,这类期权合约的生存期只有短短的一天。但是随着衍生品市场的不断发展,特别是每周期权(Weekly Options)的迅速发展,在美国股票指数期权市场中,我们每一天都可以交易到当天到期的未日期权。在了解末日期权交易之前,先让我们重温期权交易涉及的希腊值风险。
期权是金融史上人类发明的最精密的投资工具。期权的多维性给了我们几乎无数的想象空间来设计各种不同的交易策略。由于期权的多维性,在期权交易中,期权头寸的风险也不是简单的、单方面的,而是复杂的、多方面的。我们平时在期权课程中所学到的期权四个最基本的希腊值(Delta、Gamma、Vega、Theta)风险就是明证。
期权交易的四个基本希腊值风险
在期权这四个基本的希腊值风险中,Gamma可能是最不容易被初学者理解的一个。那么什么是Gamma?简单地说,Gamma是个二阶的期权风险导数,是用来观察标的产品的价格变化与期权头寸Delta值之间的变化关系。买期权(多头)不论是买看涨、买看跌,Gamma值都是正的。卖出期权头寸,不论是卖出看涨、卖出看跌,Gamma值都是负的。但Gamma和其他希腊值的关系,以及Gamma正负值的多少就是相对比较复杂的问题了。
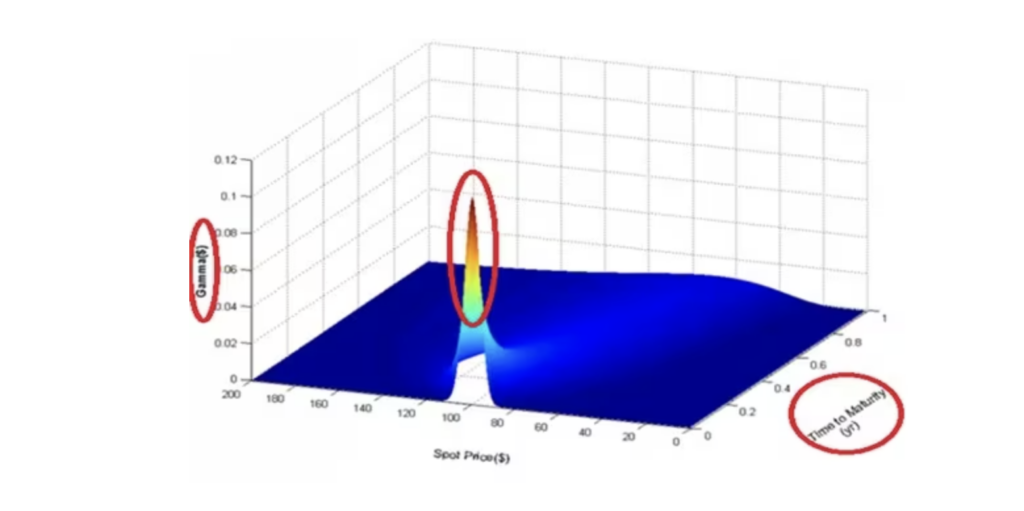
请看下面的第一张图,这是不同时间段和不同协定价格的期权头寸Gamma值。图中可以看到在接近期权到期日的前几天,平值期权的Gamma数值每日以几何级数增加,直到期权交易的最后一天(图中红色椭圆圈内)。
再看下面的第二张图,这是一张在不同时间段和不同协定价格的期权头寸Theta值的变化。图中可以看到在期权交易的最后几天,平值期权的时间价值Theta也是以几何级数的速度在不断地递减,一直到期权的最后交易时间,期权时间价值Theta归于零。
Gamma
Theta
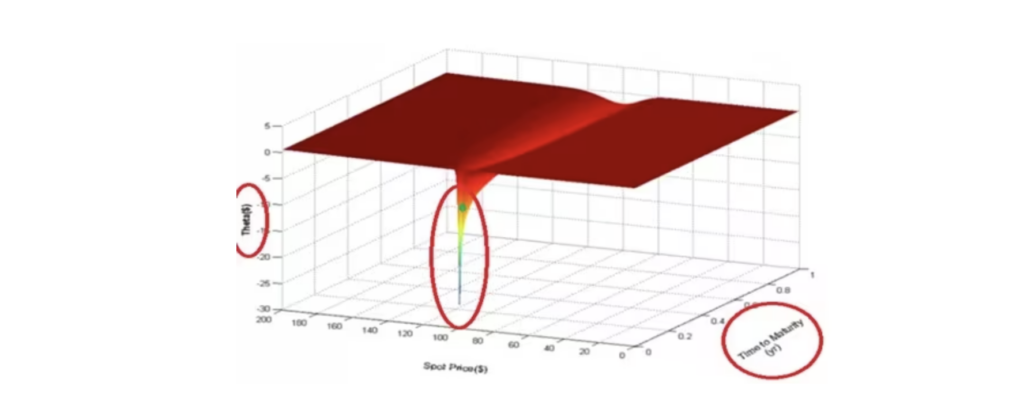
从上面这两幅图的比较,大家都可能会发现两个结论:第一个结论是Gamma和Theta基本上是鱼和熊掌不能兼得的关系。如果期权头寸具有正的Gamma值,交易中就可以得心应手的在期货市场中高抛低吸,但是这个期权头寸的时间值是负的。也就是说,随着时间的流逝,如果其他因素不变,期权的价值越来越小。第二个结论是接近期权到期日时,Gamma和Theta两个数值都以几何级数飞速增加,或者飞速减少,呈现了超短期期权交易的高度风险和收益的机会。这就是我们平时在交易中所说的“Gamma-Theta Trade off”。在期权交易中,特别是超短期期权交易中,大家需要在交易决策过程中根据Gamma和Theta的风险做出权衡,建立合理的投资仓位和策略设计。
交易末日期权的核心问题
套用到交易末日期权,也就是交易到期日的期权,从上面的两个图中,我们可以看到平值期权在到期日的Gamma和Theta风险都达到极致。而这二者的风险关系又基本上是鱼和熊掌不能兼得的关系,这就使得期权到期日的交易变得更具有挑战性和存在取得更高收益的机会。所以交易末日期权的核心问题就是:在到期日当天的短短十几个小时的交易时间中,如何处理好期权仓位的Gamma和Theta风险关系。
个人的交易经验教训是:对于末日期权最简单和风险相对比较小的交易策略是双买,也就是说,买最后一天的跨式套利(Buy Straddles)或者最后一天的宽跨(Buy Straggles)。请看下面一张图。
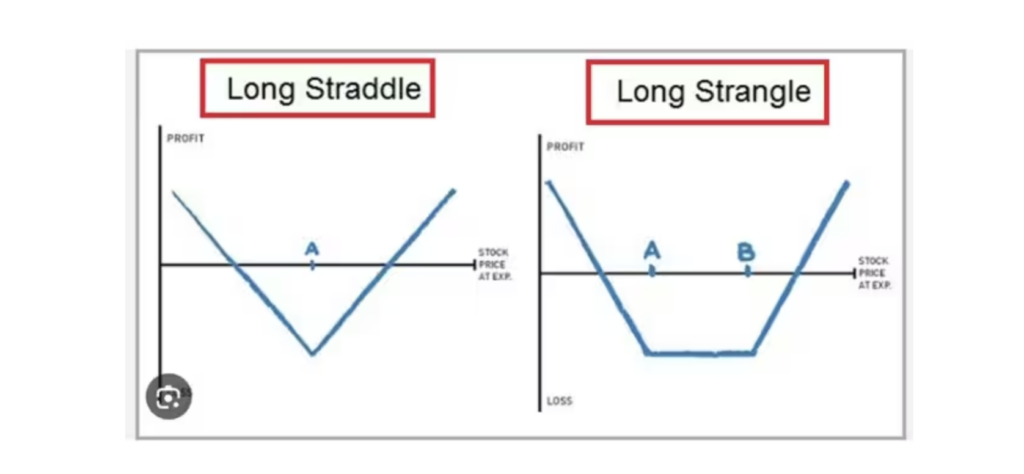
选择这一策略的理论基础是我们不知道当天市场价格的方向和可能出现的变化,就像5月19日当天由于美国两党突然停止了国家债务上限的谈判,美国股票市场价格也随之形成了180度的大转弯,但我们知道在末日期权仓位Gamma值的高度敏感性,而这一敏感性正是我们交易未日期权盈利的最好工具。
2月13日,芝商所推出微型E-迷你标普500指数(MES)和纳斯达克100指数(MNQ)每周一、周二、周三和周四到期的每周期权,加上先前推出的周五到期MES和MNQ每周期权,现在投资者每天都可以享受交易末日微型E-迷你标普500指数(MES)和纳斯达克100指数(MNQ)每周期权的挑战和乐趣了。